后缀自动机&广义后缀自动机

0x01 简单定义

对于一个自动机 $M$ 和字符串 $S = s_{0} s_{1} s_{2} ... s_{n - 1}$ 。令 $S_{i}$ 为字符串 $S$ 从第 $i$ 位开始的后缀，即 $S_{i} = s_{i} s_{i + 1} s_{i + 2} \dots s_{n - 1}$ ，如果自动机 $M$ 可以接受所有可能的 $S_{i}$ 及其子串，并排斥其他所有的字符串，那么就称这个自动机 $M$ 为字符串 $S$ 的后缀自动机。

后缀自动机全称为 Suffix Automaton，缩写为 SAM。后缀自动机非常强大，能解决所有后缀数组可以解决的问题，又因为其将字符串问题转换成了在 DAG（Directed Acyclic Graph，有向无环图）上的图论问题，所以一般来讲比后缀数组容易理解和上手。

0x02 前置知识

1. Endpos集合的定义

对于字符串 $S$ 的一个子串 $S_{ij}$ ，即 $S_{ij} = s_{i} s_{i + 1} s_{i + 2} \dots s_{j}$ ，把它在 $S$ 中出现的所有 结束位置 保存在一个集合中，这就是 Endpos集合。

如： $S = ababbaab$ ，所以 $E n d p os (ab) = {1, 3, 7}, E n d p os (b) = {1, 3, 4, 7}$ 。

2. Endpos集合的性质

(1) 如果两个子串的Endpos集合相同，那么其中一个子串必然是另一个子串的后缀

这个性质是非常显然的，只要举几个例子即可，或者我们可以反证一下：

假设两个子串的 Endpos 集合相同，而他们互不为后缀。由于 Endpos 集合存储的是结束位置，既然互不为后缀，那么结束位置肯定会出现不相等的地方，假设矛盾，原命题成立。

(2) 对于任意两个子串 $S_{i}$ 和 $S_{j}$ ，且 $∣ S_{i} ∣ \leq ∣ S_{j} ∣$ ，要么 $E n d p os (S_{j}) \subseteq E n d p os (S_{i})$ ，要么 $E n d p os (S_{i}) \cap E n d p os (S_{j}) = \emptyset$

这个性质其实是性质 (1) 的逆命题，也可以用 (1) 中类似的方法证明。

3. Endpos等价类的定义

对于所有 Endpos 集合相同的子串，我们将其归为一个 Endpos 等价类。

如： $S = ababbaab$ ，且 $E n d p os (abab) = {3}, E n d p os (bab) = {3}$ ，所以 $E n d p os (abab) = E n d p os (bab)$ ，所以子串 $abab$ 和子串 $bab$ 属于同一个 Endpos 等价类。

4. Endpos等价类的性质

(1) 对于任意一个 Endpos 等价类，将其中的子串按长度降序排列，则每个子串的长度均为上一个子串长度减 1，且为上一个子串的后缀

这个性质简单来说就是每个 Endpos 等价类中所有的子串的长度覆盖区间是连续的。

由 Endpos 集合性质 (1) 以及长度降序可知，显然每个子串是上一个子串的后缀。对于长度严格等差递减，可以这样想：

假设有一个子串 $S$ ，它的 Endpos 集合为 $A$ 。将 $S$ 依次从前面删除一个字符，首先能保证所以新得到的字符串 $S^{'}$ 都是 $S$ 的后缀，每个 $S^{'}$ 都有自己的 Endpos 集合。如果 $S^{'}$ 的 Endpos 集合仍然等于 $A$ 那么我们继续删除直到为空，如果 $S^{'}$ 已经不属于等价类 $A$ 了，那么 $S^{'}$ 自己的所有后缀都不可能属于等价类 $A$ ，因为此时 $S^{'}$ 所属的等价类 $B$ 必定至少比等价类 $A$ 多一个元素，且有关系 $A \subseteq B$ ，因为此时 $S^{'}$ 处了可以在 $S$ 中以后缀的形式出现，还可能在其他位置上出现。

(2) Endpos 等价类的数量级为 $O (n)$

这个性质其实在 SAM 中并不是那么重要，也不会对解题有什么帮助，所以在这里不会对其进行证明，但是这条性质的一个重要的结论是：对于一个长度为 $l e n$ 的字符串，其 SAM 的节点数量至少要有 $2 l e n$ 个。

5. Parent Tree 的定义

Parent Tree 这个结构是基于 Endpos 等价类的划分树结构。在前面我们已经了解了 Endpos 集合的几个性质，因为对于字符串所有的 Endpos 集合都有 不是子集就是无交集 的情况，所以对于每一个 Endpos 集合所属的 Endpos 等价类，都存在一种方法可以将其划分成另外几个存在的 Endpos 等价类，直到无法划分为止。

需要注意的是，在 SAM 中，一个Endpos集合的所有划分的并集是其子集，也就是说 可能存在Endpos集合所有划分的并集不等于其本身的情况。

如对于字符串 $S = aababa$ ，其各不同子串的 Endpos 列表及其所属 Endpos 等价类如下：

$S^{'}$	$E n d p os (S^{'})$	Endpos等价类
$ε$	${0, 1, 2, 3, 4, 5}$	0
a	${0, 1, 3, 5}$	1
aa	${1}$	2
aab	${2}$	3
aaba	${3}$	4
aabab	${4}$	5
aababa	${5}$	6
ab	${2, 4}$	7
aba	${3, 5}$	8
abab	${4}$	5
ababa	${5}$	6
b	${2, 4}$	7
ba	${3, 5}$	8
bab	${4}$	5
baba	${5}$	6

可知该字符串一共存在9个Endpos等价类，我们再按照Endpos等价类来归类这些子串：

Endpos等价类	$E n d p os (S^{'})$	$S^{'}$
0	${0, 1, 2, 3, 4, 5}$	$ε$
1	${0, 1, 3, 5}$	a
2	${1}$	aa
3	${2}$	aab
4	${3}$	aaba
5	${4}$	aabab,abab,bab
6	${5}$	aababa,ababa,baba
7	${2, 4}$	ab,b
8	${3, 5}$	aba,ba

我们从空串 $ε$ 开始划分它的 Endpos 集合，SAM 的划分过程就是 不断地往串的前面加字符。

从 $ε$ 开始，可以添加字符得到 a 和 b，我们这时候查表可以发现 $E n d p os (ε)$ 刚好能划分成 $E n d p os (a)$ 和 $E n d p os (b)$ 。

我们再从 a 开始添加字符，发现 $E n d p os (a)$ 又可以 尽可能大地 划分为 $E n d p os (aa)$ 和 $E n d p os (ba)$ ，此时会发现 $E n d p os (a)$ 中的元素 0 不存在其划分的并集中，这不重要，因为我们在前面就已经说明了原因，我们只需要保证 a 是划分代表的字符串的后缀，且划分的 Endpos 集合尽量大就行了。

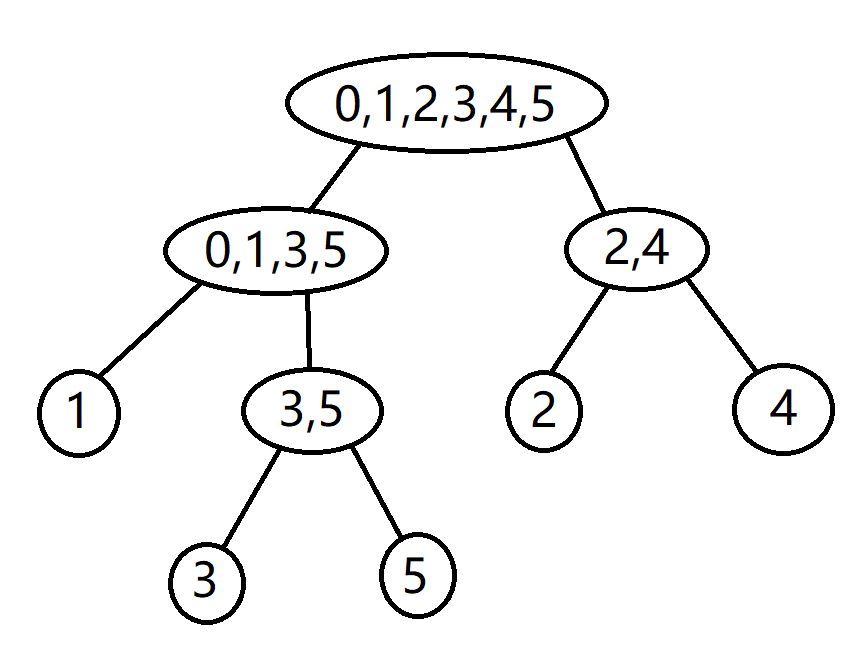
我们就如此进行划分，最后能得到这么一棵树：

这就是我们所要找的 Parent Tree，它表明了各个 Endpos 等价类之间的覆盖从属关系（父子关系），而每一条从儿子连接到父亲的边，我们称为 后缀链接。

6. Endpos等价类在Parent Tree上的关系

对于一个 Endpos 等价类 $A$ ，其中包含了若干个字符串，其中最长串的长度设为 $ma xL e n (A)$ ，最短串的长度设为 $min L e n (A)$ ，等价类 A 在 Parent Tree 上的父节点为等价类 B，则有： $min L e n (A) = ma xL e n (B) + 1$ 。

这个性质我们在上文的表中一查就能发现了，在一个等价类的最长串前面增加一个字符，那它必然属于儿子等价类中，而且是作为最短串存在的。

那么我们不需要在 Parent Tree 的每个节点里存储 Endpos 等价类的所有子串信息了，我们只需要记录该等价类最长串的长度 $l e n$ ，而最短串的长度就可以用父节点的 $l e n$ 增加 1 得到。

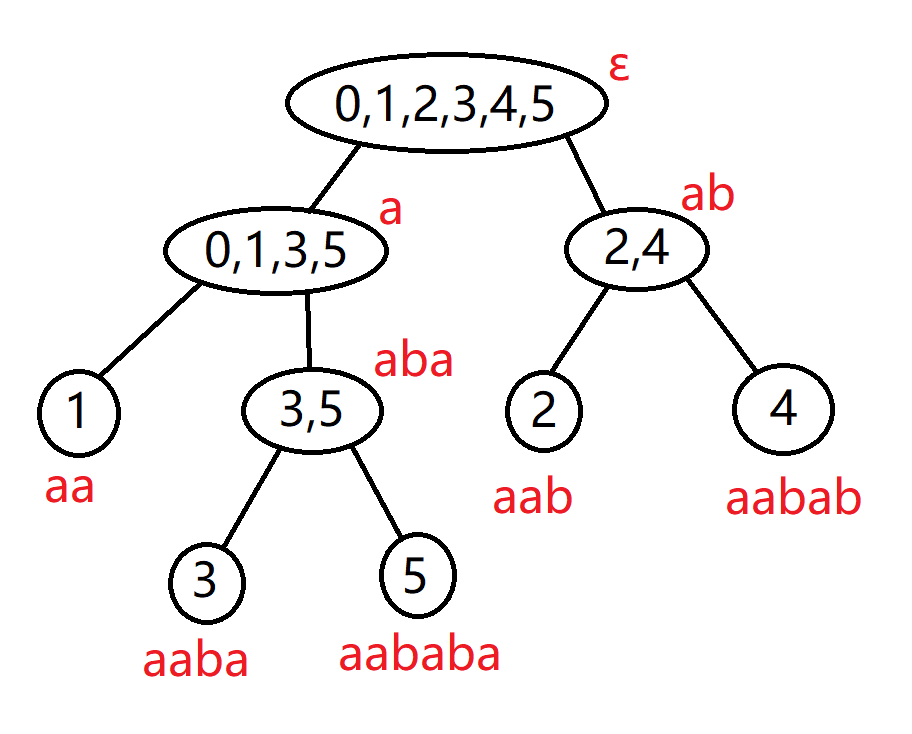
我们在上面的树形图中标注出最长串，就可以得到如下的新图：

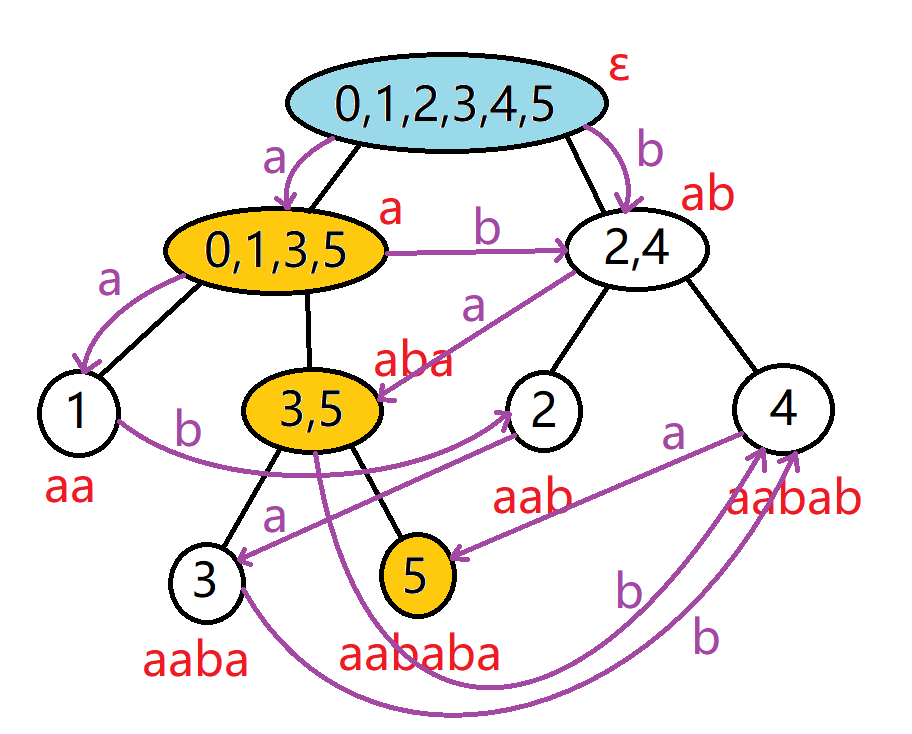
7. 将 Parent Tree 上的节点通过连接构造就能得到 SAM

~~刚刚还在讲 Parent Tree，现在突然转到 SAM，这一步是不是有点快了~~

这是最后一个前置知识。将 Parent Tree 的根节点作为 SAM 的 起始节点，将整个字符串所属的节点及其所有的，不包括起始节点父节点作为 SAM 的 终止节点，其他的节点都是 SAM 的一个状态。

我们在 Parent Tree 上建边，使每个 Endpos 等价类中的所有字符串都可以转移到达，就得到了 SAM。

至于我们构造 SAM 为啥要经过 Endpos 集合、Endpos 等价类和 Parent Tree，绕了这么一大圈，是因为我们要满足 SAM 的几个条件：有向无环图和规模最小。

我们构造出 Endpos 集合与 Endpos 等价类，并赋予他们父子关系，产生 Parent Tree，是为了满足有向无环图的要求，因为一个被父等价类所包含的等价类，它一定不可能存在一个转移回到它的父等价类中。而由于 Endpos 等价类的存在，相当于我们把字符串的所有可能转移全部压缩到了数个等价类中，这又可以满足规模最小，即状态最少的要求。

0x03 构造 SAM

老规矩，先放代码：

// 字符串长度
#define MAX_N 114514

// 字符集大小
#define MAX_M 26

// 后缀自动机结构
struct SAM {
  struct Node {
      int fa, len;    // Endpos 等价类的后缀链接和最大字符串长度
      int nxt[MAX_M]; // SAM 的状态转移边
  } T[(MAX_N << 1) + 50];

  // 节点数量计数、上一次扩展的节点位置
  int top = 1, lst = 1;

  // 插入一个后缀状态
  void insert(int x) {
    int p = lst, np = ++top;
    lst = top;
    T[np].len = T[p].len + 1;
    while (p && !T[p].nxt[x]) {
      T[p].nxt[x] = np;
      p = T[p].fa;
    }
    if (!p)
      T[np].fa = 1;
    else {
      int q = T[p].nxt[x];
      if (T[q].len == T[p].len + 1)
        T[np].fa = q;
      else {
        int nq = ++top;
        T[nq] = T[q];
        T[nq].len = T[p].len + 1;
        T[np].fa = T[q].fa = nq;
        while (p && T[p].nxt[x] == q) {
          T[p].nxt[x] = nq;
          p = T[p].fa;
        }
      }
    }
  }

  // 构造SAM
  void build(const char s[]) {
    for (int i = 0; s[i]; ++i)
      insert(s[i] - 'a');
  }
};

这是 SAM 的最基础的板子，但它却可以在每一步插入中完成构造 Endpos 等价类、更新 Parent Tree 和更新 SAM 的功能。

我们在构造 SAM 的时候直接调用 SAM::build() 函数，可以看到这个函数本质上就是按顺序把字符串的每个字符依次插入 SAM，所以真正有用的部分应该是 SAM::insert()，我们现在直接对 SAM::insert() 进行分析：

1. 新建节点

  // ...
  void insert(int x) {
    int p = lst, np = ++top;
    lst = top;
    T[np].len = T[p].len + 1;
  // ...

这段其实没什么好说的，p 会指向上一次插入的节点，np 是我们新建的节点，然后将 lst 指向我们新建的节点，因为在下一次插入时的 p' 应该指向 np。

将 T[np].len 设置为 T[p].len + 1 其实也不难理解，因为当一个字符串在末尾插入了一个新字符后，整个字符串会形成一个新的 Endpos 等价类，而这个等价类的长度就是上次插入的等价类长度加 1。

2. 调整SAM转移路径

      // ...
      while (p && !T[p].nxt[x]) {
        T[p].nxt[x] = np;
        p = T[p].fa;
      }
      // ...

我们不断地从上一个插入的位置跳转后缀链接，寻找所有没有转移到 x 字符的位置，将它们的转移指针指向新节点 np。

从上一个位置跳转后缀链接，如果你还记得我们对 SAM 的定义（不记得就点这里），就知道这实际上是在遍历上一次插入后整个 SAM 的终止节点，并检查其是否有到 x 的转移，如果没有我们就把它链接到新节点。这其实就是对旧的 Endpos 等价类进行扩展，所有旧终止节点都可以通过添加字符 x 来转移到新的状态 np。

3. 调整唯一终止节点

      // ...
      if (!p)
        T[np].fa = 1;
      // ...

如果所有的旧终止节点都可以被遍历，最后回到了起始节点，那么说明所有的终止节点都不再是终止节点（因为他们可以转移到 np），新的终止节点就只剩下了 np，这时我们把 np 的后缀链接调整到起始节点，这样下一次遍历的时候只会遍历到 np。

4. 调整新增终止节点

      // ...
      else {
        int q = T[p].nxt[x];
        if (T[q].len == T[p].len + 1)
          T[np].fa = q;
      // ...

如果有某个旧终止节点已经存在了一个字符 x 转移，那么说明这一个由字符 x 转移的节点 q 有成为新的终止节点的潜力。

这时我们检查 q 的 len 是否比其父节点 p 的 len 大 1，即 q 的 Endpos 等价类是 p 的一个最大划分，那么就可以把 np 的后缀链接调调整到 q 上了，因为此时 q 也是一个合法的结束状态。

需要注意的是，在 q 成为终止节点后，原来 p 后缀链接上的部分终止节点就不再是终止节点了，新的终止节点遍历将经过 q 而走 q 的后缀链接，因为 Endpos 等价类的划分关系发生了改变。

5. 调整节点关系

          // ...
          else {
            int nq = ++top;
            T[nq] = T[q];
            T[nq].len = T[p].len + 1;
            T[np].fa = T[q].fa = nq;
            while (p && T[p].nxt[x] == q) {
              T[p].nxt[x] = nq;
              p = T[p].fa;
            }
          }
          // ...

如果 q 的 Endpos 等价类不是 p 的一个最大划分，那么我们需要新建一个中间节点了，让这个节点成为 p 的最大划分。

我们需要从 q 等价类继承一部分信息构造 nq，首先就是令 T[nq].len 等于 T[p].len+1，表明等价类 nq 是 p 的一个新划分，在那之前我们还把 q 的所有状态转移赋予了 nq，因为此时我们本质上是让 nq 成为 p 的一个最大划分，从 p 到 q 再继续转移本质上与从 p 到 nq 再继续转移是一样的。

然后我们调整 np 和 q 的后缀链接为 nq，对 np 来说，就相当于第 (4) 步，对于 q 来说，就相当于更新了等价类从属关系，它本身会成为 nq 的一个划分。

最后我们还是遍历 p 的后缀链接，把所有链接到 q 上的转移换成链接到 nq 上，本质上还是把 q 替换成 nq 操作。

构造 SAM 其实就是两步，新建节点 + 调整路径。

0x04 广义后缀自动机（GSAM）

广义后缀自动机 GSAM（General Suffix Automaton）是 SAM 家族的另一大神器，它可以用来解决多字符串后缀自动机问题。

GSAM 依赖于一棵 Trie 树，并在遍历 Trie 树的过程中建立一个后缀自动机。为此我们其实只需要对普通的 SAM 代码进行一些修改：

// 字符串长度
#define MAX_N 114514

// 字符集大小
#define MAX_M 26

// 广义后缀自动机结构
struct GSAM {
  struct Node {
    int fa, len;    // Endpos等价类的后缀链接和最大字符串长度
    int nxt[MAX_M]; // SAM的状态转移边
  } T[(MAX_N << 1) + 50];

  // 节点数量计数
  int top = 1;

  // 从给定的位置插入一个后缀状态
  int insert(int x, int lst) {
    // 特判
    if (T[lst].nxt[x]) {
      int p = lst, q = T[lst].nxt[x];
      if (T[q].len == T[p].len + 1)
        return q;
      int nq = ++top;
      T[nq] = T[q];
      T[nq].len = T[p].len + 1;
      T[q].fa = nq;
      while (p && T[p].nxt[x] == q) {
        T[p].nxt[x] = nq;
        p = T[p].fa;
      }
      return nq;
    }

    // 和SAM一样
    int p = lst, np = ++top;
    T[np].len = T[p].len + 1;
    while (p && !T[p].nxt[x]) {
      T[p].nxt[x] = np;
      p = T[p].fa;
    }
    if (!p)
      T[np].fa = 1;
    else {
      int q = T[p].nxt[x];
      if (T[q].len == T[p].len + 1)
        T[np].fa = q;
      else {
        int nq = ++top;
        T[nq] = T[q];
        T[nq].len = T[p].len + 1;
        T[np].fa = T[q].fa = nq;
        while (p && T[p].nxt[x] == q) {
          T[p].nxt[x] = nq;
          p = T[p].fa;
        }
      }
    }

    // 记得返回
    return np;
  }
};

主要修改部分就是 GSAM::insert()，该函数每次会返回上一次输入字符的节点编号，同时也要求输入一个节点编号作为 lst 执行插入。

GSAM 和 SAM 最大的不同其实就是开头的那一段：

      // ...
      if (T[lst].nxt[x]) {
        int p = lst, q = T[lst].nxt[x];
        if (T[q].len == T[p].len + 1)
          return q;
        int nq = ++top;
        T[nq] = T[q];
        T[nq].len = T[p].len + 1;
        T[q].fa = nq;
        while (p && T[p].nxt[x] == q) {
          T[p].nxt[x] = nq;
          p = T[p].fa;
        }
        return nq;
      }
      // ...

其实非常好理解，就相当于你要插入的位置本来就已经存在了一个转移，那么就可以如法炮制，用构造 SAM 时的第5步那样处理就行了，当然你还需要注意返回值是什么。

既然 GSAM::insert() 已经被修改了，那么构造方式当然也要变：

// 遍历Trie树
void dfs(int u, int lst) {
  // 将Trie节点u所代表的的字符插入到GSAM中
  lst = gsam.insert(s[u] - 'a', lst);
  // 遍历Trie子节点
  for (int i = 0; i < MAX_M; ++i)
    if (trie[u][i])
      dfs(trie[u][i], lst);
}

这样一来，我们的 GSAM 中就存储了整个 Trie 树的后缀信息，然后你就可以把 GSAM 当做普通的 SAM 来用了。

当然构造 GSAM 除了使用 dfs 以外，还可以使用 bfs，只需要稍微改一改 dfs 代码就行了，此处不再给出。

除了这种 Trie 树和 GSAM 主结构分开的的形式，还有一种直接在 Trie 树上构造 GSAM 的形式，这种形式可以省去一个 Trie 的空间：

// 字符串长度
#define MAX_N 114514

// 字符集大小
#define MAX_M 26

// 广义后缀自动机结构
struct GSAM {
  struct Node {
    int fa, len;    // Endpos等价类的后缀链接和最大字符串长度
    int nxt[MAX_M]; // SAM的状态转移边
  } T[(MAX_N << 1) + 50];

  // 节点数量计数
  int top = 1;

  // 插入Trie树
  void insertTrie(const char s[]) {
    int j = 1;
    for (int i = 0, x; s[i]; ++i) {
      x = s[i] - 'a';
      if (!trie[j][x])
        trie[j][x] = ++top;
      j = trie[j][x];
    }
  }

  // 插入GSAM
  int insertGSAM(int x, int lst) {
    int p = lst, np = T[lst].nxt[x];
    T[np].len = T[p].len + 1;
    p = T[p].fa;
    while (p && !T[p].nxt[x]) {
      T[p].nxt[x] = np;
      p = T[p].fa;
    }
    if (!p)
      T[np].fa = 1;
    else {
      int q = T[p].nxt[x];
      if (T[q].len == T[p].len + 1)
        T[np].fa = q;
      else {
        int nq = ++top;
        T[nq] = T[q];
        T[nq].len = T[p].len + 1;
        T[np].fa = T[q].fa = nq;
        while (p && T[p].nxt[x] == q) {
          T[p].nxt[x] = nq;
          p = T[p].fa;
        }
      }
    }
    return np;
  }
  
  // 构造GSAM
  void build() {
    std::queue<std::pair<int, int>> que;
    for (int i = 0; i < MAX_M; ++i)
      if (trie[1][i])
        que.emplace(i, 1);
    while (!que.empty()) {
      auto tmp = que.front();
      que.pop();
      int lst = insertGSAM(tmp.first, tmp.second);
      for (int i = 0; i < MAX_M; ++i)
        if (T[lst].nxt[i])
          que.emplace(i, lst);
    }
  }
};

首先是插入 Trie 树的 GSAM::insertTrie()，相信大家都明白，然后我们看看经过了修改的 GSAM::insertGSAM()，可以发现其实大部分和我们上面的第一份 GSAM 的 GSAM::insert() 是一样的，唯一不同点是这里：

  // ...
  int insertGSAM(int x, int lst) {
    int p = lst, np = T[lst].nxt[x];
    T[np].len = T[p].len + 1;
    p = T[p].fa;
  // ...

由于我们是直接在 Trie 树上建的 GSAM，所以当我们在 lst 插入 x 节点时，实际上要调整的节点是 T[lst].nxt[x]，所以我们直接调整把这个节点当做普通 SAM 插入的节点即可，至于后面为什么还要 p = T[p].fa，这也很显然，因为下面的 while 循环会判断一次 T[p].nxt[x]，如果不提前修改 p 的话，那循环就会直接退出，也就没起到遍历上一次插入的终止节点的作用了。

然后是构造 GSAM 的 GSAM::build()，我们可以看到，其实这就是我们第一份 GSAM 构造代码的 BFS 版本，所以解释意义如上一样。

0x05 伪广义自动机

伪广义自动机 ~~PGSAM（Pseudo General Suffix Automaton）~~（没有这种缩写），是指用一些奇淫技巧使 SAM 能够拥有 GSAM 的功能，但是其构造并不符合标准 GSAM 的要求。

伪广义自动机可以使用如下两种构造方法：

将不同的字符串之间用一个 特殊且唯一 的符号隔开，连接成一个全新的字符串，然后用其来构造 SAM
在插入一个字符串后，将 SAM 的 lst 重置为 1

虽然这两种操作都很简单，但是他们就是可以得到正确的答案，所以被称为 伪广义自动机。

伪广义自动机是 复杂度危险 的，一般情况下尽量不要使用，除非遇到了某些要求苛刻的题目（如卡 Trie 树的空间），才使用伪广义自动机。

0x06 后缀自动机的应用

1. 检查一个字符串是否为子串

这个非常简单，因为 SAM 中存储了字符串所有的后缀信息，所以只需要在 SAM 上跑匹配，如果走到了一个不存在的节点，那么该字符串一定不是子串。

2. 计算一个字符串本质不同的子串数量

这个也很简单，因为 SAM 的每个节点存储一个 Endpos 等价类，每个 Endpos 等价类中的字符串长度是有序的，且各个 Endpos 等价类都是不同的，那么问题的答案就是所有 Endpos 等价类的字符串数量之和。

而在 Parent Tree 上，一个 Endpos 等价类 A 的大小是： $ma xL e n (A) - min L e n (A) + 1$ ，也就是： $ma xL e n (A) - ma xL e n (f a (A))$ ，其中 fa(A) 代表等价类 A 在 Parent Tree 上的父节点。

所以答案就是： $\sum (ma xL e n (i) - ma xL e n (f a (i)))$

例题：生成魔咒 - bzoj4516

3. 计算一个字符串本质不同的子串长度和

和上一题一模一样，只不过把计数变成了计算长度，那么一个Endpos等价类A的长度和就是：

\frac{ma xL e n ( A ) \cdot ( ma xL e n ( A ) + 1 ) - ma xL e n ( f a ( A )) \cdot ( ma xL e n ( f a ( A )) + 1 )}{2}

总和就是：

\sum \frac{ma xL e n ( i ) \cdot ( ma xL e n ( i ) + 1 ) - ma xL e n ( f a ( i )) \cdot ( ma xL e n ( f a ( i )) + 1 )}{2}

4. 字典序第 k 大子串

这个问题上本质上是求 SAM 上字典序第大的路径，这就要求我们统计每个节点的路径总数，然后寻找第 k 大。

我们可以根据 $ma xL e n$ 对每个节点进行一次 拓扑排序，然后根据拓扑序倒推每个节点的路径数量。

一个节点的路径数量为：

s u m [i] = 1 + j \in V_{i} \sum s u m [j]

其中 $j$ 为 $i$ 的子节点。

例题：SPOJ - SUBLEX

5. 最小循环移位

~~这题其实用最小表示法计算更快更方便~~

易知对于字符串 $S$ ，新字符串 $SS$ 显然包含了 $S$ 所有的循环移位方案，那么我们只需要对 $SS$ 构造 SAM，然后贪心地在 SAM 上走最小的节点，直到走的长度为 $∣ S ∣$ 为止。

6. 子串的出现次数

~~除非查询次数多且子串长度长，否则这题用 KMP 更好~~

设需要查询的子串为 $P$ ，我们只需要在 SAM 上匹配这个子串，如果走到了不存在的节点，那么说明该子串不存在，否则我们可以到达一个节点，而这个节点的 Endpos 等价类大小就是 $P$ 的出现次数。

7. 子串第一次出现的位置

~~不推荐理由同上，除非条件苛刻否则 KMP 走起~~

对于每个节点维护一个数组 first[] 表示这个 Endpos 等价类中最短串的首位置。

在 SAM 插入操作过程中，当新建节点 np 时，我们令 first[np] = T[np].len - 1，当新建节点 nq 时，我们令 first[nq] = first[q]。

经过如上预处理操作后，对于子串 $P$ ，我们在 SAM 上匹配这个串，直到在某个节点 x 上结束，查询的结果就是 $f i rs t [x] - ∣ P ∣ + 1$ 。

8. 子串所有的出现位置

~~不推荐理由同上，除非条件苛刻否则 KMP 走起~~

前面的操作与 7 中相同，但是我们在预处理的过程中还需要记录节点在 Parent Tree 上的子节点。

我们仍旧最后会在一个节点 x 处停下，并输出第一次出现的位置，但是接下来我们需要遍历 x 节点在 Parent Tree 上的子树，一旦找到了终止节点，那么我们还需要输出一次答案，这样我们才能得到所有出现的位置。

9. 两个字符串的最长公共子串

设两个字符串 $S_{1}$ 、 $S_{2}$ ，我们对 $S_{1}$ 构造 SAM，然后用 $S_{2}$ 在 SAM 上进行匹配，我们需要维护两个变量 $u$ 和 $l$ ，分别代表当前节点编号和当前匹配长度。

一开始令 u = 1, l = 0，然后扫描 $S_{2}$ ，对于第 $i$ 个字符 $c$ ：

如果存在从 $u$ 到 $c$ 的转移，那么直接转移并使 $l$ 增加1
如果不存在，那么我们就沿着后缀链接走，缩短匹配的长度，即：u = T[u].fa, l = T[u].len
如果此时 $u$ 已经到达了起始状态 1，那么令 l = 0 表示字符 $c$ 根本没在 $S_{1}$ 中出现过

我们不断扫描并执行以上三种动作，并不停更新记录 $l$ 的最大值，直到扫描完成，这时候最大值就是两个字符串的最长公共子串长度。

如果你想得到最长公共子串，那么只需要在最大值更新的时候同时记录位置信息即可。

10. 多个字符串的最长公共子串

和求两个字符串的最长公共子串差不多，对第一个字符串建 SAM，然后用其他字符串在上面匹配，但我们需要保存在每个节点 $u$ 上所算得的 $l$ 。

我们将每轮字符串匹配所算得的 $l$ 保存在 $t m p_{u}$ 中，在当前字符串都匹配完了之后，用 $t m p_{u}$ 更新当前节点 $u$ 的 $l$ 最小值，记为 $mi n_{u}$ ，最终的答案就是 $max {mi n_{u}}$ 。

但是在每次 $t m p_{u}$ 更新之后，其实 $t m p_{f a (u)}$ 也需要更新，因为父节点 $f a (u)$ 本质上是 $u$ 的后缀子串，当 $u$ 有了更长的匹配，那么 $f a (u)$ 的最长匹配应该从 $u$ 那里继承，所以在每轮字符串匹配完成后，我们需要跑一边拓扑序，把所有节点的父节点长度 $t m p_{f a (u)}$ 更新，然后再去更新 $mi n_{u}$ 。

需要注意的是，我们需要将 $mi n_{u}$ 初始化为 $l e n_{u}$ 因为一个状态的最长公共子串不可能比它所代表的 Endpos 等价类最长串还要长。

如果还你不太懂，这是一份AC代码。

0x07 最后的话

当你做多了 SAM 的题目之后，你会发现有个东西 —— 拓扑排序 是经常用到的。

SAM 最后形成的图是一个 DAG，所以一定存在这么一个拓扑序，而它能很好地反映各个节点之间的拓展关系。然后出题人就会在拓扑序的基础上套 DP 了。然后就是万物皆可 DP。

当然 SAM 上的拓扑排序不需要像普通拓扑排序一样统计什么入度信息，而是 直接对每个节点以 len 进行一次基数排序即可，因为我们保证了 DAG 上的父子节点之间的 len 值一定是有序的。

又因为拓扑序的存在，我们就可以把图上搜索统计的一些题目通过拓扑序改成线性统计了，这样极大地提高了计算的效率。

最后贡献一份 SAM 拓扑排序的代码：

  // ...
  // 基数排序用的桶、存储拓扑序的数组
  int bk[], tp[];
  void topology() {
    for (int i = 1; i <= top; ++i)
      ++bk[T[i].len];
    for (int i = 1; i <= top; ++i)
      bk[i] += bk[i - 1];
    for (int i = 1; i <= top; ++i)
      tp[bk[T[i].len]--] = i;
  }
  // ...

0x08 题单

题目	难度	备注
生成魔咒 - bzoj4516	1	SAM模板题，本质不同子串数量
SPOJ - NSUBSTR	1	SAM模板题，节点路径总数问题
SPOJ - LCS	2	SAM模板题，最长公共子串长度
SPOJ - SUBLEX	2	SAM模板题，第k大子串
诸神眷顾的幻想乡 - bzoj3926	2	GSAM模板题，本质不同子串数量
差异 - bzoj3238	3	SAM+树形DP
Good Article Good sentence - HDU4416	3	伪广义自动机，本质不同子串数量
SPOJ - LCS2	3	SAM多字符串最长公共子串
世界线 - bzoj2894	4	GSAM第k大子串
str2int - HDU4436	4	GSAM上拓扑排序构造不同子串进行计数
找相同字符 - bzoj4566	5	SAM+DP

0x09 鸣谢

史上最通俗的后缀自动机详解 - KesdiaelKen 的博客 - 洛谷博客
 后缀自动机 (SAM) - OI Wiki
广义后缀自动机 - OI Wiki

寒夏摸鱼站

Live your dream, and share your passion.

后缀自动机&广义后缀自动机

0x01 简单定义

0x02 前置知识

1. Endpos集合的定义

2. Endpos集合的性质

(1) 如果两个子串的Endpos集合相同，那么其中一个子串必然是另一个子串的后缀

(2) 对于任意两个子串 $S_{i}$ 和 $S_{j}$ ，且 $∣ S_{i} ∣ \leq ∣ S_{j} ∣$ ，要么 $E n d p os (S_{j}) \subseteq E n d p os (S_{i})$ ，要么 $E n d p os (S_{i}) \cap E n d p os (S_{j}) = \emptyset$

3. Endpos等价类的定义

4. Endpos等价类的性质

(1) 对于任意一个 Endpos 等价类，将其中的子串按长度降序排列，则每个子串的长度均为上一个子串长度减 1，且为上一个子串的后缀

(2) Endpos 等价类的数量级为 $O (n)$

5. Parent Tree 的定义

6. Endpos等价类在Parent Tree上的关系

7. 将 Parent Tree 上的节点通过连接构造就能得到 SAM

0x03 构造 SAM

1. 新建节点

2. 调整SAM转移路径

3. 调整唯一终止节点

4. 调整新增终止节点

5. 调整节点关系

0x04 广义后缀自动机（GSAM）

0x05 伪广义自动机

0x06 后缀自动机的应用

1. 检查一个字符串是否为子串

2. 计算一个字符串本质不同的子串数量

3. 计算一个字符串本质不同的子串长度和

4. 字典序第 k 大子串

5. 最小循环移位

6. 子串的出现次数

7. 子串第一次出现的位置

8. 子串所有的出现位置

9. 两个字符串的最长公共子串

10. 多个字符串的最长公共子串

0x07 最后的话

0x08 题单

0x09 鸣谢

后缀自动机&广义后缀自动机

0x01 简单定义

0x02 前置知识

1. Endpos集合的定义

2. Endpos集合的性质

(1) 如果两个子串的Endpos集合相同，那么其中一个子串必然是另一个子串的后缀

(2) 对于任意两个子串 Si​ 和 Sj​，且 ∣Si​∣≤∣Sj​∣，要么 Endpos(Sj​)⊆Endpos(Si​)，要么 Endpos(Si​)∩Endpos(Sj​)=∅

3. Endpos等价类的定义

4. Endpos等价类的性质

(1) 对于任意一个 Endpos 等价类，将其中的子串按长度降序排列，则每个子串的长度均为上一个子串长度减 1，且为上一个子串的后缀

(2) Endpos 等价类的数量级为 O(n)

5. Parent Tree 的定义

6. Endpos等价类在Parent Tree上的关系

7. 将 Parent Tree 上的节点通过连接构造就能得到 SAM

0x03 构造 SAM

1. 新建节点

2. 调整SAM转移路径

3. 调整唯一终止节点

4. 调整新增终止节点

5. 调整节点关系

0x04 广义后缀自动机（GSAM）

0x05 伪广义自动机

0x06 后缀自动机的应用

1. 检查一个字符串是否为子串

2. 计算一个字符串本质不同的子串数量

3. 计算一个字符串本质不同的子串长度和

4. 字典序第 k 大子串

5. 最小循环移位

6. 子串的出现次数

7. 子串第一次出现的位置

8. 子串所有的出现位置

9. 两个字符串的最长公共子串

10. 多个字符串的最长公共子串

0x07 最后的话

0x08 题单

0x09 鸣谢

(2) 对于任意两个子串 $S_{i}$ 和 $S_{j}$ ，且 $∣ S_{i} ∣ \leq ∣ S_{j} ∣$ ，要么 $E n d p os (S_{j}) \subseteq E n d p os (S_{i})$ ，要么 $E n d p os (S_{i}) \cap E n d p os (S_{j}) = \emptyset$

(2) Endpos 等价类的数量级为 $O (n)$