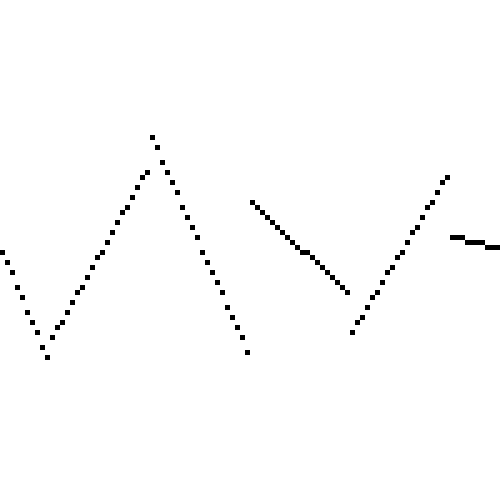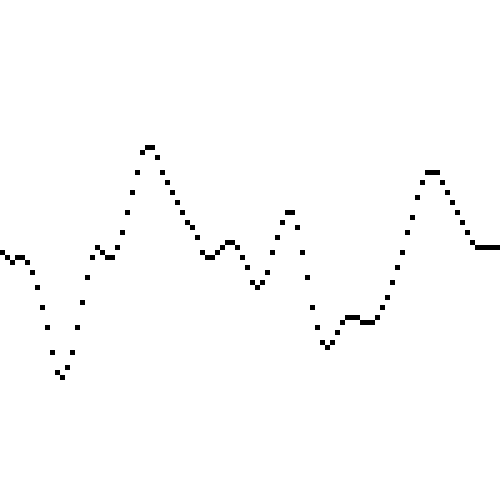柏林噪声是由 Ken Perlin 于 1983 年发明的一种自然噪声算法。之所以称之为自然噪声，是因为其可以很好地模拟自然纹理，如水波、火焰、大理石纹路等，也可以用于生成动态烟雾等各种特效。柏林噪声和德国没有任何关系

基本原理

柏林噪声所运用的基本原理其实非常简单，三个词语就可以概括：随机、点积 和 插值。

随机指的是柏林噪声需要根据生成的维度先产生一张随机梯度图谱，表示这个点的梯度趋势。如一维噪声需要一张一维随机向量表，二维噪声需要一张二维的随机二维向量表，以此类推，柏林噪声可以产生任意维度的噪声图谱。需要注意的是，我们的随机梯度图谱需要是随机的 N 维单位长度向量，除了一维的情况 —— 你需要的是介于 -1 和 1 之间的随机标量。

我们得到了随机梯度图谱，但这张图谱由于是完全随机的，所以其毫无变化与过度可言。实际上，柏林噪声是在这张梯度图谱中平滑插值得到的，但在此之前，我们需要先对梯度进行处理，这就是点积的由来。对于一个插值点，我们需要先找到它所有邻近的梯度点，一维就是左右两个，二维就是周围四个，三维就是周围八个……然后计算出插值点到这些梯度点之间的距离向量 —— 拿插值点的坐标减去梯度点的坐标。最后把每个梯度向量与其对应的距离向量点乘在一起，得到的标量就是该梯度点对插值点的影响因子。

最后一步插值，我们得到所有邻近点的影响因子，然后用插值函数，计算得到该插值点的最终噪声值。

有时候为了让噪声更加自然或更加曲折，我们还会生成多张柏林噪声，然后按照一定的比例将这些噪声叠加合成起来变成一张最终的噪声图谱。

随机数的生成

一般情况下，随机数的生成并不是什么主要问题，但我们有个小语境 —— 游戏。大家玩肉鸽或者 Minecraft 这类地图随机性高的游戏时，一般都会接触地图种子这个说法，其实这就是一个随机数一切的开始。

针对于不同的游戏类型，我们的随机数表生成也有所不同，但是他们都离不开伪随机数，伪随机数是保证游戏种子一致性的关键，因为伪随机数是可以预测的。

对于地图有限的游戏，我们可以直接利用种子预先生成地图所使用的随机数表，然后再进行插值。这种直接预生成随机一般使用的伪随机算法都非常经典，如线性插值法和 MT 算法。这两种算法一种实现非常方便，且生成快速，一种则是各种语言标准库的标配，随机分布均匀。

而对于如 Minecraft 等地图近乎无限大的游戏，则无法通过预生成随机表的方法来生成游戏地图了，更多的是采用坐标变换的方法，将坐标转换为伪随机数，以保证生成结果只和随机数种子与坐标有关系。其实最简单的方法就是拿坐标点作为随机种子，然后套用上面的算法生成第 X 个随机数：

class random_sys
{
public:
  random_sys(uint64_t seed, uint64_t step):
    seed_(seed), step_(step)
  {}

  uint64_t rand(uint64_t x, uint64_t y)
  {
    std::mt19937_64 mt(seed_ * x ^ y);
    for (uint64_t i = 0; i < step_; ++i)
    {
      mt();
    }
    return mt();
  }

private:
  uint64_t seed_, step_;
};

我们用上面的随机生成器，以 114514 为种子，跳过步长为 2，生成一张 100x100 的随机噪声图，坐标从 $(0,0)$ 到 $(100,100)$：

再以 114514 为种子，跳过步长为 5，生成一张 100x100 的随机噪声图：

然后以 19260817 为种子，跳过步长为 5，生成一张规格一样的随机噪声图：

可以看到即使是简单的生成策略，也能产生不错的随机效果。

插值算法

柏林噪声中的插值算法一般都是根据维度方向分别进行插值，如二维情况下需要分别在横向和纵向进行两次插值才能得到最终点的值。其次，这种基于维度方向的插值都是在两点之间进行的，所以两点之间的插值算法就很多了。

如最邻近插值法，简单比较插值点与数据点之间的距离，取距离短的值作为插值。这种方法优点是简单快速，缺点是过渡很生硬。

double NNI(Point a, Point b, double x)
{
  if (fabs(a.x - x) < fabs(b.x - x))
  {
    return a.y;
  }
  else 
  {
    return b.y;
  }
}

然后就是线性插值法，在两点之间连接一条线段，直接通过构造函数得到插值点的值。如果是二维插值，那么先对于 x 方向的 4 个点两两进行插值，得到两个点，再对这两个点于 y 方向上插值，得到最终点，最终会进行三次线性插值。这样虽然增大了计算量，但是大大改善了插值过渡的平滑程度。

double LI(Point a, Point b, double x)
{
  return a.y + (x - a.x) * (b.y - a.y) / (b.x - a.x);
}

如果将上述的线性算法换成其他函数，如三角函数、缓动函数……那么你可以得到其他插值算法，使得过渡更加平滑。

double SI(Point a, Point b, double x)
{
  return a.y + (b.y - a.y) * (1 - cos((x - a.x) / (b.x - a.x) * PI)) / 2;
}

从一维开始

我们按照柏林噪声的生成步骤进行三步走，来生成一张类似于泰拉瑞亚的一维地形：

double SI(double pct)
{
  static const double PI = acos(-1);
  return (1 - cos(pct * PI)) / 2;
}

double perlin(const random_sys& rnd, double x, double f)
{
  // Spread
  x /= f;

  // Get adjacent gradient point
  uint64_t x0 = x;
  uint64_t x1 = x0 + 1;

  // Get gradient in [-1, 1] with 256 level
  double y0 = ((int)(rnd.rand(x0) % 257) - 128) / 128.0;
  double y1 = ((int)(rnd.rand(x1) % 257) - 128) / 128.0;

  // Get position vector
  double v0 = x - x0;
  double v1 = x - x1;

  // Get dot product
  double d0 = v0 * y0;
  double d1 = v1 * y1;

  // Interpolate
  double y = d0 + SI((double)(x - x0) / (x1 - x0)) * (d1 - d0);

  return y;
}

以上代码我们使用了正弦插值函数 SI()，主要函数 perlin() 通过输入一个伪随机生成器、一个坐标和坐标散布三个参数，输出一个噪声值。坐标散布你可以近似地理解为两个相邻的梯度点之间有多少个插值点，我们的生成器经过了散布、获得相邻梯度坐标、获得梯度值、计算位移向量、计算点积和插值一共六步，得到一个一维柏林噪声。

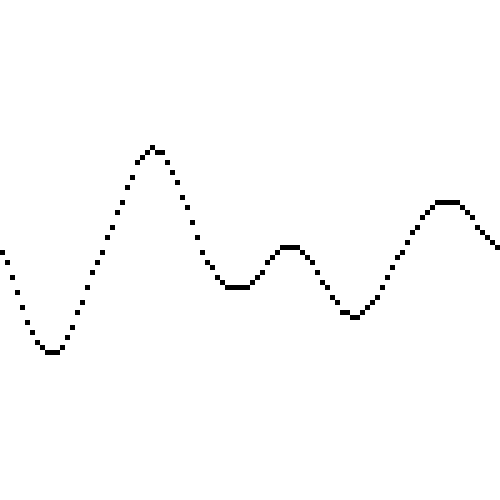
以 19260817 为种子，跳过步长为 5，散布为 20，插值函数为正弦插值，生成坐标从 0 到 100，得到的趋势图如下：

我们使用不同的插值函数，如最邻近插值：

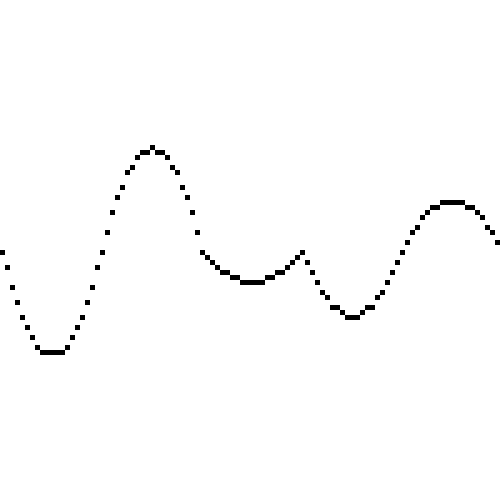
线性插值：

可见正弦插值的效果最好，最邻近插值效果最差，线性插值在一些大拐角的地方会出现不平滑的尖锐点。

当然我们可以叠加多个一维柏林噪声，使地形更加多变。如下我们在上面的正弦插值噪声叠加了一个以 114514 为种子，跳过步长为 2，散布为 10 的新柏林噪声：

进入二维

二维柏林噪声的生成和一维差不多，只不过需要运算的点多了一倍：

struct Vec2
{
  double x, y;
};

double perlin(const random_sys& rnd, const Vec2& pos, double f)
{
  // Spread
  Vec2 t = {pos.x / f, pos.y / f};

  // Get adjacent gradient point
  uint64_t gx[2], gy[2];
  gx[0] = t.x;
  gx[1] = gx[0] + 1;
  gy[0] = t.y;
  gy[1] = gy[0] + 1;

  // Get gradient
  Vec2 g[4];
  for (int i = 0; i < 4; ++i)
  {
    double ang = ((int)(rnd.rand(gx[(i >> 1) & 1], gy[i & 1]) % 257) - 128) / 128.0 * PI;
    g[i] = {cos(ang), sin(ang)};
  }

  // Get position vector
  Vec2 v[4];
  for (int i = 0; i < 4; ++i)
  {
    v[i] = {t.x - gx[(i >> 1) & 1], t.y - gy[i & 1]};
  }

  // Get dot product
  double d[4];
  for (int i = 0; i < 4; ++i)
  {
    d[i] = v[i].x * g[i].x + v[i].y * g[i].y;
  }

  // Interpolate
  double a1 = d[0] + SI((double)(t.y - gy[0]) / (gy[1] - gy[0])) * (d[1] - d[0]);
  double a2 = d[2] + SI((double)(t.y - gy[0]) / (gy[1] - gy[0])) * (d[3] - d[2]);
  double b = a1 + SI((double)(t.x - gx[0]) / (gx[1] - gx[0])) * (a2 - a1);

  return b;
}

大致过程都是差不多的，只不过我们把生成随机梯度向量改成生成随机角度然后生成对应的单位向量，其次是最后的插值，由于我们已经在二维平面，所以插值要沿横向和纵向进行，最终体现为三次插值。

以 19260817 为种子，跳过步长为 5，散布为 20，插值函数为正弦插值，生成坐标从 $(0,0)$ 到 $(100,100)$，得到的趋势图如下：

同样，你可以叠加更多的二维柏林噪声来制造起伏细节效果，这里就不再演示了。

我们还可以继续来试一试其他插值函数，这是线性插值函数的：

这是最邻近插值函数的：

所以，最好还是选择各类缓动函数作为插值函数，这样子可以使得柏林噪声的过渡比较好。

小结

地形生成只是游戏地图生成的一个小点，之后我们将讨论更多种的地图生成技术。